
Mathematics is the truth someone could demonstrate
S.G.
Scope: This web site underlines some basics mathematics theory from the following topics: arithmetic, algebra, geometry, trigonometry (in construction), calculus (in construction), all needed for studying more advanced topics.
In the future the topics will be listed for various grades.(for now the web site is under construction, and its display may not be pleased to the eye, but the focus was on the math knowledge and solving techniques than on the web design)
NOTE: For now you need to scroll down to see the exercises. In the future you will need to click the topic and it will pop up. The Back to Top does not work yet.
Arithmetics and Algebra
Basic things you need to know in Mathematics-Arithmetics
- Set of Numbers: N, W, I, Q, nonQ, R, C; Examples
- Adding, subtracting, multiplying, dividing positive and negative numbers Examples
- Simplify the math expressions with brackets Examples
- Fractions and decimal numbers Examples
- Factor numbers, find the common factors between numbers and math expressionsExamples
- Powers, and calculations of mathematical expressions using exponentsExamples
- Radicals, and calculations using radicalsExamples
- Percentage, calculations and word problems using percentagesExamples
Basic things you need to know in Mathematics-Algebra
- Simplify expressions with variables. Addition, subtraction, multiplication, divisionExamples
- Solve equations with 1 variableExamples
Medium Mathematics Knowledge - Algebra
- Solve and graph linear equationsExamples
- Solve and graph systems of 2 linear equationsExamples
- Solve equations with 3 variables
- Solve inequalities
- Solve Quadratics. Graph quadraticsExamples
- Polynomial Functions. Graphs. Word problems
- LogarithmsExamples
Back to top
Geometry
Test your knowledge in Geometry 2D
LINEs and ANGLES
- A line is made by infinity of points
- Each side of a line could be considered a 180 degrees angle
- Three points are on a line if they can form an 180 degrees angle
- Parallel lines intersected by a secant form pair of equal angles (internal, alternate, corespondent)
- If two lines intersected by a secant form at least a pair of equal angles (internal, alternate, corespondent types), the two lines are parallel
- Two perpendicular lines on the 3rd one are parallel
- If one of the two parallel lines is perpendicular on a 3rd line, than the other parallel is perpendicular on the 3rd one
- The shortest distance from a point to a line is the perpendicular from that point to the line
- The angles with parallel lines are equal or supplementary (their sum is 180 degrees)
- The angles with perpendicular sides are equal
- The bigger the angle in a triangle, the larger the opposite side
- Three parallel lines intersected by 2 secants form equal segment ratios (Thales Theorem)
- The angle with the vertex in the center of the circle and the sides chords in the circle has the same measurement with the circle arc between its sides.
- The distance from a point to a line is the measurement of the perpendicular from that point to the line
- The bisector of an angle is the line which divides the angle in two equal angles
- The perpendicula bisector is a line perpendicular on the middle of a segment
- All the points on a perpendicular bisector are equaly distanced to the segment ends
Back to top
TRIANGLES
- The types of triangles: scalene, isosceles, right triangle, equilateral
- The sum of interior angles of a triangle is 180 degrees
- In a triangle, the sum of two sides is bigger than the third side
- In a triangle, the difference of two sides is smaller than the third side
- The exterior angle of a triangle is formed by the elongation of one side and another side of the triangle
- The measurement of the exterior angle of a triangle is equal with the sum of the measurements of the interior angles of the triange non-adjacent to it
- The important lines in a triangle are: the height or altitude, the bisector, the median and the perpendicular bisector
- The height is the line started from a triangle vertex and ends perpendicular on the oposite site
- The area of a triangle is the (height x base)/2, and it is the same for all the heights and bases used
- All the three heights of a triangle intersect in a single point, H, named orthocenter. Note: if the triangle has an obtuse angle the heights intersect outside the triangle
- The bisector in a triangle intersects the oposite side, and makes a ratio of the segments created equal with the ratio of the sides starting from its vertex
- The three bisectors in a triangle intersect in a single point, the center of the inscribed circle in the triangle in the triangle
- The three medians in a triangle intersect in a single point, G, called the center of mass. It is located at 2/3 from the vertex and 1/3 from the base of the triangle
- All the heights of a right triangle intersect in the 90 degree vertex
- Any triangle can be circumscribed to a circle
- The center of the circle circumscribed to a triangle is found at the intersection of the triangle perpendicular bisectors
- Any triangle can be inscribed in a circle
- The center of the circle inscribed in a triangle, is found at the intersection of triangle bisectors
- The middle line in a triangle joins the middles of two sides in a triangle. It is parallel to the third side and half of its length
- In a triangle, the sum of two sides is bigger than the third side
- In a triangle, the sum of two sides is bigger than the third side
Back to top
Geometry 3D - basic theorems
- 3 non-colinear points determine an unique plane
- A line not contained in the plane is parallel with the plane if it is parallel with any line in the plane
- A line is contained in a plane if it has 2 point contained in the plane
- A line is perpendicular on a plane if it is perpendicular on any line in the plane
- A line is perpendicular on the plane if it is perpendicular on 2 intersecting lines contained in the plane
- The angle between a line and a plane is the one formed by the line and its projection on the plane
- The angle between 2 planes is the angle between 2 lines, each contained by one of the plane, and perpendicular on their intersection line
- If the intersection line of 2 planes is perpendicular on the 3rd one, than the 2 planes are perpendicular on the 3rd one
- The theorem of the 3 perpendiculars. Draw a line d1 perpendicular on a plane P, with the intersection M. Draw a random line d2 in the plane P, not intersecting line d1. Draw a perpendicular line from point M on line d2, and mark the intersection with N. Than any line draw from any point on line d1 joining point N is perpendicular on line d2. The reciprocals are true.
Back to top
Set of Numbers Examples
 Back to top
Back to top
Operations with Numbers
 Back to top
Back to top
Expressions with Brackets
 Back to top
Back to top
Fractions and Decimal Numbers
 Back to top
Back to top
 Back to top
Back to top
 Back to top
Back to top
 Back to top
Back to top
 Back to top
Back to top
Factoring Numbers
 Back to top
Back to top
 Back to top
Back to top
Powers of Numbers and Radicals written as Powers
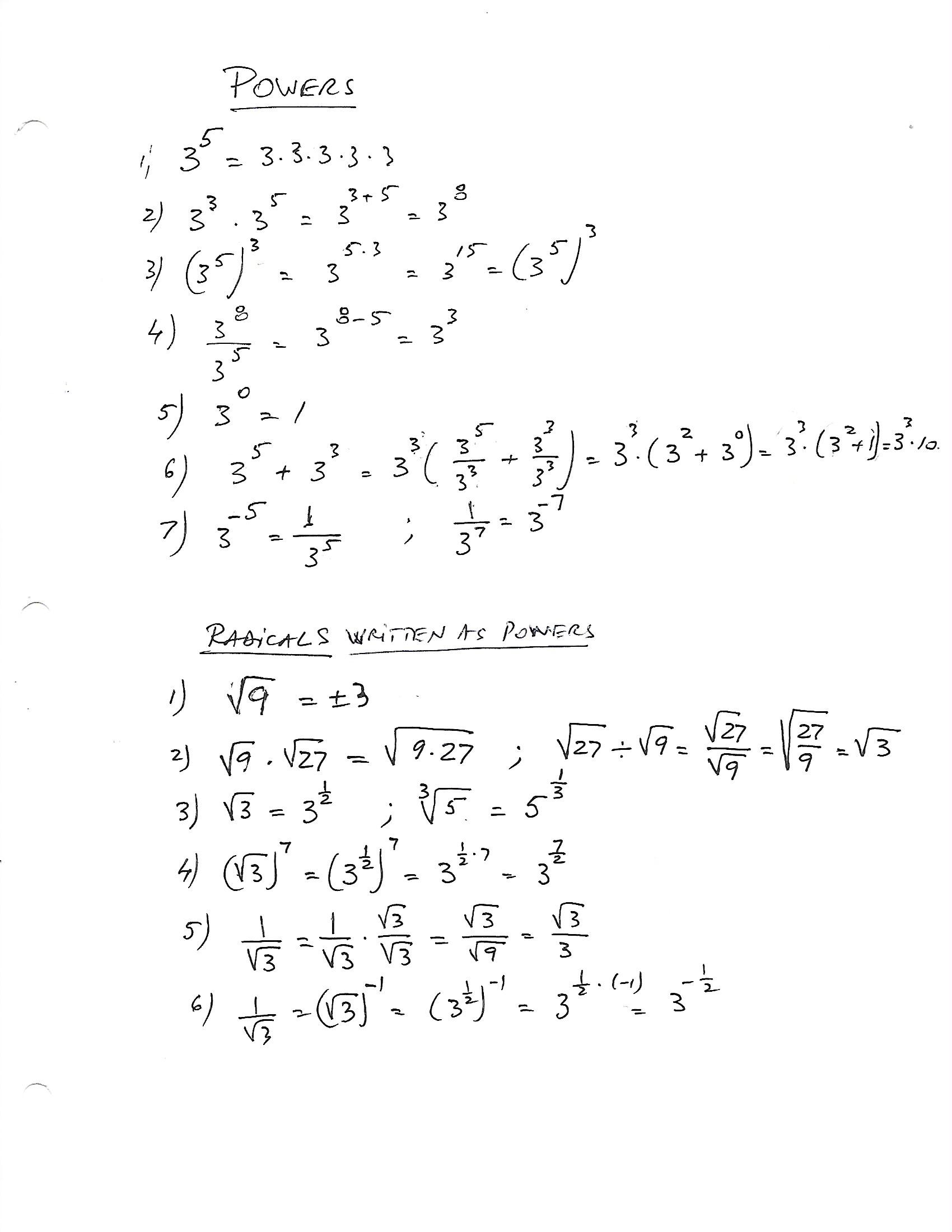 Back to top
Back to top
Radicals
 Back to top
Back to top
Percentages
 Back to top
Back to top
Expressions with Variables
 Back to top
Back to top
2D Geometry Tips
 Back to top
Back to top
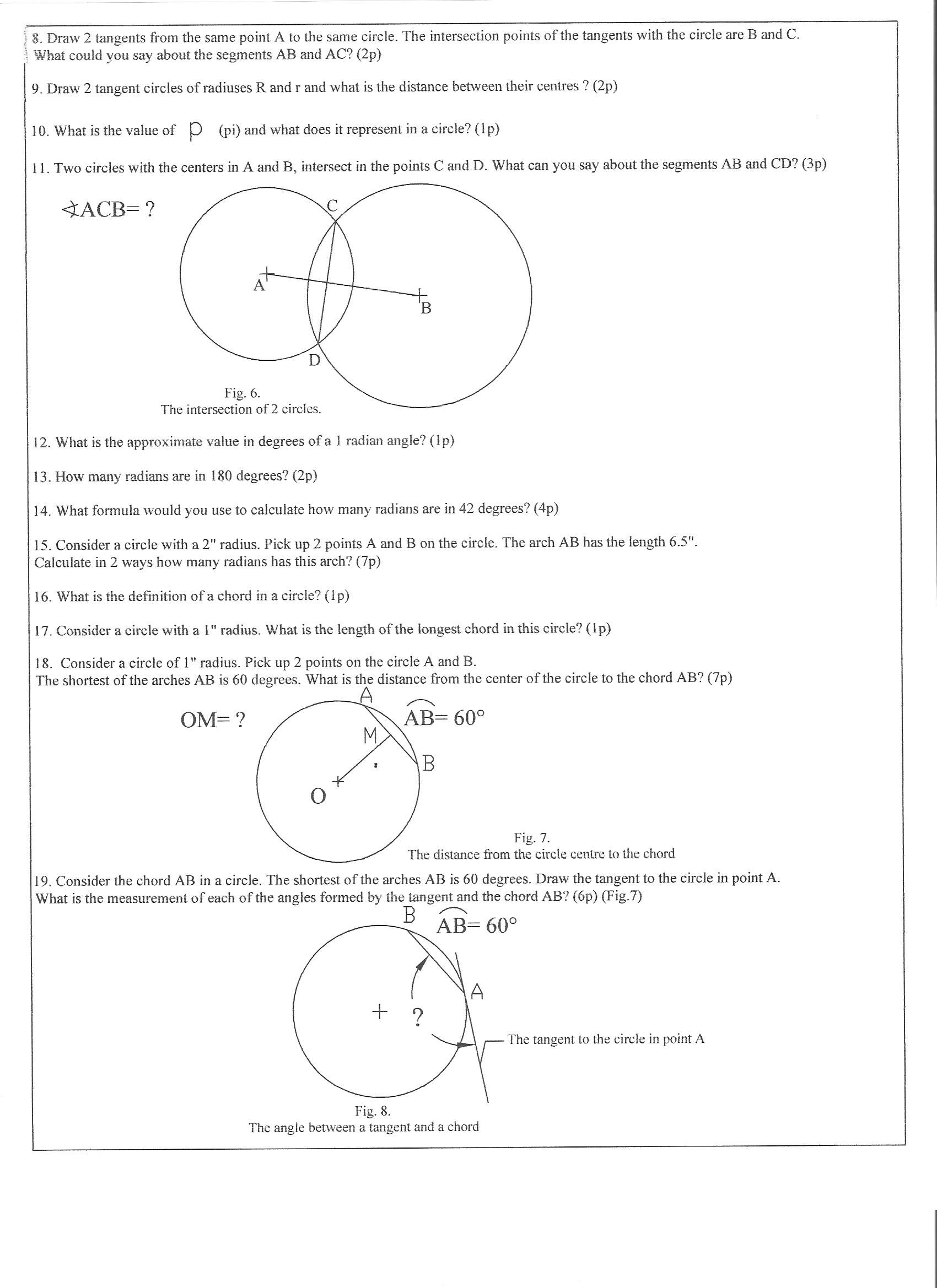
Test Your Knowledge in 2D Geometry
 Back to top
Back to top
 Back to top
Back to top
 Back to top
Back to top
 Back to top
Back to top
 Back to top
Back to top
 Back to top
Back to top
 Back to top
Back to top
Equations with one Variable
 Back to top
Back to top
Theory and Examples for Logarithms
 Back to top
Back to top
Theory and Examples for Linear Equations
 Back to top
Back to top
Theory and Examples for Systems of Linear Equations
 Back to top
Back to top
Quadratics Solve and Graph
 Back to top
Back to top
Ontario Ministry of Education Curriculum Back to top




 Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top  Back to top
Back to top